Tỉ số lượng giác là gì? - Đại số

Chào quý khách, thời điểm ngày hôm nay bản thân đăng bài xích vì như thế với vướng mắc về một yếu tố tôi đã học tập ở lớp 9. Như title nội dung bài viết, bản thân thiếu hiểu biết ra làm sao là tỉ con số giác. Tất nhiên là tôi đã biết sin = $\frac{đối}{huyền}$,... tuy nhiên bản thân ko biết thành phẩm cơ kể từ đâu nhưng mà với. Vả lại, nếu như tớ bấm máy: sin(30) thì = $\frac{1}{2}$. Mình không hiểu biết nhiều thành phẩm này được xem ra làm sao, liệu với cơ hội nào là rất có thể tính được nó ko nên dùng PC không? Mong chúng ta trả lời hùn bản thân. Xin cảm ơn trước   

Bài ghi chép và đã được sửa đổi nội dung vì chưng Tongkhangte: 05-08-2017 - 08:09

Chào quý khách, thời điểm ngày hôm nay bản thân đăng bài xích vì như thế với vướng mắc về một yếu tố tôi đã học tập ở lớp 9. Như title nội dung bài viết, bản thân thiếu hiểu biết ra làm sao là tỉ con số giác. Tất nhiên là tôi đã biết sin = $\frac{đối}{huyền}$,... tuy nhiên bản thân ko biết thành phẩm cơ kể từ đâu nhưng mà với. Vả lại, nếu như tớ bấm máy: sin(30) thì = $\frac{1}{2}$. Mình không hiểu biết nhiều thành phẩm này được xem ra làm sao, liệu với cơ hội nào là rất có thể tính được nó ko nên dùng PC không? Mong chúng ta trả lời hùn bản thân. Xin cảm ơn trước   

từ xưa lắm rr.

cái này chỉ mất học tập nằm trong bảng tính sin cot tag cos thì mới có thể k người sử dụng máy thôi

Chào quý khách, thời điểm ngày hôm nay bản thân đăng bài xích vì như thế với vướng mắc về một yếu tố tôi đã học tập ở lớp 9. Như title nội dung bài viết, bản thân thiếu hiểu biết ra làm sao là tỉ con số giác. Tất nhiên là tôi đã biết sin = $\frac{đối}{huyền}$,... tuy nhiên bản thân ko biết thành phẩm cơ kể từ đâu nhưng mà với. Vả lại, nếu như tớ bấm máy: sin(30) thì = $\frac{1}{2}$. Mình không hiểu biết nhiều thành phẩm này được xem ra làm sao, liệu với cơ hội nào là rất có thể tính được nó ko nên dùng PC không? Mong chúng ta trả lời hùn bản thân. Xin cảm ơn trước   

Mình với cơ hội này sẽ không biết giành được không

bạn rất có thể thăm dò hiểu ở đây https://vi.wikipedia...wiki/Lượng_giác  hoặc  ở trên đây https://vi.wikipedia.../Hàm_lượng_giác  còn nếu khách hàng căn vặn vì sao sin(30) =$\frac{1}{2}$, thì tớ với kiểu mẫu này 

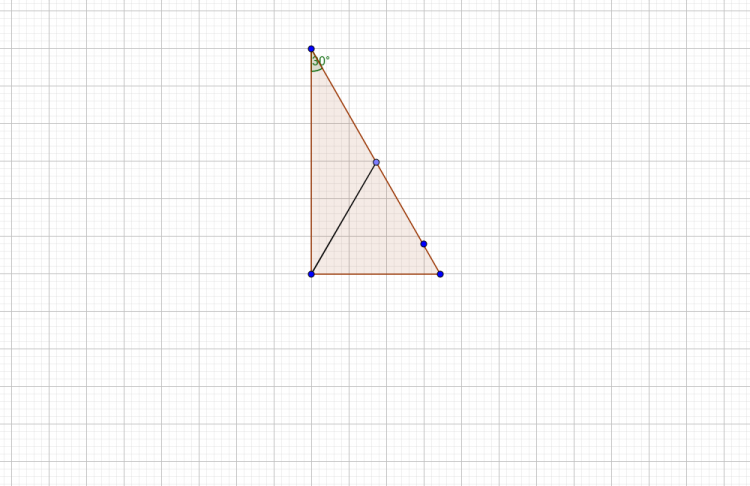
Bạn tiếp tục rất có thể CM t/c vô tam giác vuông, đàng trung tuyến ứng vs cạnh huyền =$\frac{1}{2}$ cạnh huyền bằng phương pháp gấp hai đương trung tuyến rồi CM , thế là xong

, Công việc tiếp sau chúng ta CM tam giác mặt mũi cân nặng bên dưới là tam giác đều -> cạnh góc vuông mặt mũi dưới= 50% cạnh huyền ->...

Tất nhiên là tôi đã phát âm qua loa bao nhiêu trang cơ rồi, hiểu không còn rồi. Chỉ vướng mắc là kẻ tớ đo lường và tính toán ra làm sao thôi.

Vậy nếu như góc ko nên là 30 thì sao? Nếu nó là 45 thì thành phẩm tiếp tục là $\frac{\sqrt{2}}{2}$. 

Rồi nếu như kể từ sin$^{-1}($$\frac{\sqrt{2}}{2}$) làm thế nào gửi trở nên số ngay sát vì chưng với 30?.

Mong chúng ta trả lời hùn bản thân. 

Bài ghi chép và đã được sửa đổi nội dung vì chưng Tongkhangte: 05-08-2017 - 10:41

Tất nhiên là tôi đã phát âm qua loa bao nhiêu trang cơ rồi, hiểu không còn rồi. Chỉ vướng mắc là kẻ tớ đo lường và tính toán ra làm sao thôi.

Vậy nếu như góc ko nên là 30 thì sao? Nếu nó là 45 thì thành phẩm tiếp tục là $\frac{\sqrt{2}}{2}$. 

Rồi nếu như kể từ sin$^{-1}($$\frac{\sqrt{2}}{2}$) làm thế nào gửi trở nên số ngay sát vì chưng với 30?.

Mong chúng ta trả lời hùn bản thân. 

Để chứng tỏ sin(45)=$\frac{\sqrt{2}}{2}$ chúng ta vẽ tam giác vuông cân nặng đi ra rồi người sử dụng tấp tểnh lí Py-ta-go CM cạnh huyền$^{2}$ = $2a^{2}$ (a là cạnh góc vuông)  từ cơ -> đpcm , bản thân ko học tập thâm thúy về lượng giác lắm nên ko thể phân tích và lý giải bao nhiêu kiểu mẫu thâm thúy xa vời nên khao khát chúng ta cảm thông

Tất nhiên là tôi đã phát âm qua loa bao nhiêu trang cơ rồi, hiểu không còn rồi. Chỉ vướng mắc là kẻ tớ đo lường và tính toán ra làm sao thôi.

Vậy nếu như góc ko nên là 30 thì sao? Nếu nó là 45 thì thành phẩm tiếp tục là $\frac{\sqrt{2}}{2}$. 

Rồi nếu như kể từ sin$^{-1}($$\frac{\sqrt{2}}{2}$) làm thế nào gửi trở nên số ngay sát vì chưng với 30?.

Mong chúng ta trả lời hùn bản thân. 

Tính toán như thế nào à ? Vấn đề này có tương quan đến Toán học cao cấp. Mình sẽ cố gắng trình bày theo đuổi cách dễ hiểu ngầm nhất.

Đầu tiên là nói về đơn vị đo góc.

Ở trung học cơ sở, tớ chỉ quen thuộc với đơn vị đo góc là độ, phút, giây. Lên trung học phổ thông, tớ sẽ làm quen thuộc với đơn vị khác là radian ($rad$)

Ta hãy vẽ một hình tròn bán kính $R$ với góc ở tâm bằng $\alpha$.

Nếu $\alpha =90^o$ thì nó sẽ chắn một cung tròn có độ dài là $\frac{2\pi R}{4}=\frac{\pi}{2}\ R$

Nếu $\alpha =180^o$ thì nó sẽ chắn một cung tròn có độ dài là $\frac{2\pi R}{2}=\pi R$

Nếu $\alpha =60^o$ thì nó sẽ chắn một cung tròn có độ dài là $\frac{2\pi R}{6}=\frac{\pi}{3}\ R$

..................................................

..................................................

Từ đó suy đi ra :

Nếu $\alpha =a^o$ thì nó sẽ chắn một cung tròn có độ dài là $\frac{2\pi R.a}{360}=\frac{a\pi}{180}\ R$

Người tớ gọi góc $90^o$ là góc $\frac{\pi}{2}$ radian ; góc $180^o$ là góc $\pi$ radian ; góc $60^o$ là góc $\frac{\pi}{3}$ radian (chữ radian viết tắt là rad, tuy nhiên thường thì bỏ hẳn, ko viết, mà ngầm hiểu ngầm là tính bằng rad)

Như vậy góc $a^o$ sẽ đổi thành $\frac{a\pi}{180}$ (rad)

Bây giờ, xét một góc có số đo là $x$ (rad).

Từ thế kỷ 18, người tớ đã tìm được các công thức sau :

$\sin x\approx x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}-...$

$\cos x\approx 1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\frac{x^8}{8!}-...$

(trong đó $k!=1.2.3.4...(k-1).k$)

Tuy trên đây chỉ là các công thức giao động tuy nhiên càng lấy nhiều số hạng thì độ chính xác càng cao. Còn việc tìm đi ra các công thức này thì có tương quan đến phép khai triển Maclaurin là cái mà người mua hàng sẽ học ở Đại học.

Thời đó ko có máy tính nên để xây dựng các bảng sin, cos... các nhà toán học đều phải tính bằng tay (thủ công)

Để xây dựng một bảng sin, cos với 4 chữ số sau dấu phẩy (loại mà tớ thường thấy in bên trên giấy bán ở nhà sách), các nhà toán học đã dùng 2 công thức ở bên trên với 5 số hạng đầu tiên (phải tính đủ 5 số hạng thì mới có được kết quả với sai số dưới $0,00005$). Như vậy, lập được bảng lượng giác 4 chữ số sau dấu phẩy mang đến các góc cách nhau $6'$ bằng thủ công quả là một "kỳ công"

Ngày ni, các công thức bên trên đã được lập trình mang đến máy tính nên tớ chỉ là bấm bấm vài cái là đã có kết quả với độ chính xác rất cao.

Bài ghi chép và đã được sửa đổi nội dung vì chưng chanhquocnghiem: 05-08-2017 - 14:04

Tính toán như thế nào à ? Vấn đề này có tương quan đến Toán học cao cấp. Mình sẽ cố gắng trình bày theo đuổi cách dễ hiểu ngầm nhất.

Đầu tiên là nói về đơn vị đo góc.

Ở trung học cơ sở, tớ chỉ quen thuộc với đơn vị đo góc là độ, phút, giây. Lên trung học phổ thông, tớ sẽ làm quen thuộc với đơn vị khác là radian ($rad$)

Ta hãy vẽ một hình tròn bán kính $R$ với góc ở tâm bằng $\alpha$.

Nếu $\alpha =90^o$ thì nó sẽ chắn một cung tròn có độ dài là $\frac{2\pi R}{4}=\frac{\pi}{2}\ R$

Nếu $\alpha =180^o$ thì nó sẽ chắn một cung tròn có độ dài là $\frac{2\pi R}{2}=\pi R$

Nếu $\alpha =60^o$ thì nó sẽ chắn một cung tròn có độ dài là $\frac{2\pi R}{6}=\frac{\pi}{3}\ R$

..................................................

..................................................

Từ đó suy đi ra :

Nếu $\alpha =a^o$ thì nó sẽ chắn một cung tròn có độ dài là $\frac{2\pi R.a}{360}=\frac{a\pi}{180}\ R$

Người tớ gọi góc $90^o$ là góc $\frac{\pi}{2}$ radian ; góc $180^o$ là góc $\pi$ radian ; góc $60^o$ là góc $\frac{\pi}{3}$ radian (chữ radian viết tắt là rad, tuy nhiên thường thì bỏ hẳn, ko viết, mà ngầm hiểu ngầm là tính bằng rad)

Như vậy góc $a^o$ sẽ đổi thành $\frac{a\pi}{180}$ (rad)

Bây giờ, xét một góc có số đo là $x$ (rad).

Từ thế kỷ 18, người tớ đã tìm được các công thức sau :

$\sin x\approx x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}-...$

Xem thêm: Công viên Thủ Lệ - Điểm đến không thể bỏ lỡ ở Hà Nội

$\cos x\approx 1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\frac{x^8}{8!}-...$

(trong đó $k!=1.2.3.4...(k-1).k$)

Tuy trên đây chỉ là các công thức giao động tuy nhiên càng lấy nhiều số hạng thì độ chính xác càng cao. Còn việc tìm đi ra các công thức này thì có tương quan đến phép khai triển Maclaurin là cái mà người mua hàng sẽ học ở Đại học.

Thời đó ko có máy tính nên để xây dựng các bảng sin, cos... các nhà toán học đều phải tính bằng tay (thủ công)

Để xây dựng một bảng sin, cos với 4 chữ số sau dấu phẩy (loại mà tớ thường thấy in bên trên giấy bán ở nhà sách), các nhà toán học đã dùng 2 công thức ở bên trên với 5 số hạng đầu tiên (phải tính đủ 5 số hạng thì mới có được kết quả với sai số dưới $0,00005$). Như vậy, lập được bảng lượng giác 4 chữ số sau dấu phẩy mang đến các góc cách nhau $6'$ bằng thủ công quả là một "kỳ công"

Ngày ni, các công thức bên trên đã được lập trình mang đến máy tính nên tớ chỉ là bấm bấm vài cái là đã có kết quả với độ chính xác rất cao.

Thật sự thì tôi cũng mong muốn hiểu thâm thúy về những tỉ con số giác này, cực kỳ thú vị. Nếu được, bạn cũng có thể cho bản thân hiểu thêm về luật lệ khai triển Maclaurin và công thức bên trên được không? 

Thật sự thì tôi cũng mong muốn hiểu thâm thúy về những tỉ con số giác này, cực kỳ thú vị. Nếu được, bạn cũng có thể cho bản thân hiểu thêm về luật lệ khai triển Maclaurin và công thức bên trên được không? 

Vì ko biết trình độ người mua hàng lớp mấy nên trước Khi nói về khai triển Maclaurin, mình xin xỏ nói sơ về các hàm số $y=\sin x$, $y=\cos x$ và các đạo hàm của chúng.

Ở trung học cơ sở, tớ chỉ biết $\sin$ và $\cos$ các góc từ $0$ đến $90^o$. Lên trung học phổ thông, người tớ mở rộng tập xác định của chúng đi ra toàn tập $\mathbb{R}$. Như vậy các hàm $y=\sin x$ và $y=\cos x$ có tập xác định là $\mathbb{R}$ (lưu ý $x$ ở trên đây tính bằng $rad$)

Hàm $y=\sin x$ có đạo hàm là $\cos x$ ; còn hàm $y=\cos x$ có đạo hàm là $-\sin x$

Trong toán học cao cấp, có định lý như thế này :

Cho $a$ và $b$ là 2 số thực thỏa mãn $a< 0<b$.

Nếu hàm $f(x)$ xác định vô $[a;b]$, có đạo hàm hữu hạn đến cấp n+1 vô $(a;b)$ thì vô $[a;b]$, hàm $f(x)$ có thể khai triển như sau :

$f(x)=f(0)+\frac{f'(0)}{1!}\ x+\frac{f''(0)}{2!}\ x^2+...+\frac{f^{(n)}(0)}{n!}\ x^n+\frac{f^{(n+1)}(c)}{(n+1)!}\ x^{n+1}$

(trong đó $c$ là một giá trị thích hợp nằm giữa $0$ và $x$)

Đây gọi là khai triển Maclaurin. Số hạng cuối cùng có giá trị tuyệt đối rất nhỏ so sánh với giá trị tuyệt đối của các số hạng khác nên có thể viết

$f(x)\approx f(0)+\frac{f'(0)}{1!}\ x+\frac{f''(0)}{2!}\ x^2+...+\frac{f^{(n)}(0)}{n!}\ x^n$

Bây giờ xét hàm $f(x)=\sin x$, tớ có $f(0)=0$ ; $f'(0)=1$ ; $f''(0)=0$ ; $f'''(0)=-1$ ; ... (cứ tuần hoàn như thế)

Thay vào thì sẽ có công thức giao động của $\sin x$ như ở bên trên cơ.

Nếu xét hàm $f(x)=\cos x$, thì $f(0)=1$ ; $f'(0)=0$ ; $f''(0)=-1$ ; $f'''(0)=0$ ; ... (cũng tuần hoàn tương tự)

Thay vào cũng sẽ có công thức giao động của $\cos x$ như ở bên trên cơ.

Bằng phương pháp này, người tớ chi tiết thể khai triển rất nhiều hàm khác nữa.

Tính toán như thế nào à ? Vấn đề này có tương quan đến Toán học cao cấp. Mình sẽ cố gắng trình bày theo đuổi cách dễ hiểu ngầm nhất.

Đầu tiên là nói về đơn vị đo góc.

Ở trung học cơ sở, tớ chỉ quen thuộc với đơn vị đo góc là độ, phút, giây. Lên trung học phổ thông, tớ sẽ làm quen thuộc với đơn vị khác là radian ($rad$)

Ta hãy vẽ một hình tròn bán kính $R$ với góc ở tâm bằng $\alpha$.

Nếu $\alpha =90^o$ thì nó sẽ chắn một cung tròn có độ dài là $\frac{2\pi R}{4}=\frac{\pi}{2}\ R$

Nếu $\alpha =180^o$ thì nó sẽ chắn một cung tròn có độ dài là $\frac{2\pi R}{2}=\pi R$

Nếu $\alpha =60^o$ thì nó sẽ chắn một cung tròn có độ dài là $\frac{2\pi R}{6}=\frac{\pi}{3}\ R$

..................................................

..................................................

Từ đó suy đi ra :

Nếu $\alpha =a^o$ thì nó sẽ chắn một cung tròn có độ dài là $\frac{2\pi R.a}{360}=\frac{a\pi}{180}\ R$

Người tớ gọi góc $90^o$ là góc $\frac{\pi}{2}$ radian ; góc $180^o$ là góc $\pi$ radian ; góc $60^o$ là góc $\frac{\pi}{3}$ radian (chữ radian viết tắt là rad, tuy nhiên thường thì bỏ hẳn, ko viết, mà ngầm hiểu ngầm là tính bằng rad)

Như vậy góc $a^o$ sẽ đổi thành $\frac{a\pi}{180}$ (rad)

Bây giờ, xét một góc có số đo là $x$ (rad).

Từ thế kỷ 18, người tớ đã tìm được các công thức sau :

$\sin x\approx x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}-...$

$\cos x\approx 1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\frac{x^8}{8!}-...$

(trong đó $k!=1.2.3.4...(k-1).k$)

Tuy trên đây chỉ là các công thức giao động tuy nhiên càng lấy nhiều số hạng thì độ chính xác càng cao. Còn việc tìm đi ra các công thức này thì có tương quan đến phép khai triển Maclaurin là cái mà người mua hàng sẽ học ở Đại học.

Thời đó ko có máy tính nên để xây dựng các bảng sin, cos... các nhà toán học đều phải tính bằng tay (thủ công)

Để xây dựng một bảng sin, cos với 4 chữ số sau dấu phẩy (loại mà tớ thường thấy in bên trên giấy bán ở nhà sách), các nhà toán học đã dùng 2 công thức ở bên trên với 5 số hạng đầu tiên (phải tính đủ 5 số hạng thì mới có được kết quả với sai số dưới $0,00005$). Như vậy, lập được bảng lượng giác 4 chữ số sau dấu phẩy mang đến các góc cách nhau $6'$ bằng thủ công quả là một "kỳ công"

Ngày ni, các công thức bên trên đã được lập trình mang đến máy tính nên tớ chỉ là bấm bấm vài cái là đã có kết quả với độ chính xác rất cao.

Xin lỗi chúng ta, tuy nhiên thực sự bản thân thiếu hiểu biết tại phần, vì như thế sao đơn vị chức năng là radian?  . Nếu người sử dụng bảng lượng giác hoặc người sử dụng PC thì sin(90$^{o}$) = 1, hoặc cos(45$^{o}$) = $\frac{\sqrt{2}}{2}$. Nếu đơn vị chức năng là chừng thì công thức bên trên nên đổi khác chăng?

Bài ghi chép và đã được sửa đổi nội dung vì chưng Tongkhangte: 05-08-2017 - 19:35

Xin lỗi chúng ta, tuy nhiên thực sự bản thân thiếu hiểu biết tại phần, vì như thế sao đơn vị chức năng là radian?  . Nếu người sử dụng bảng lượng giác hoặc người sử dụng PC thì sin(90$^{o}$) = 1, hoặc cos(45$^{o}$) = $\frac{\sqrt{2}}{2}$. Nếu đơn vị chức năng là chừng thì công thức bên trên nên đổi khác chăng?

Trong bảng lượng giác hoặc vô máy tính đều có 2 loại đơn vị đo góc.

Đối với máy tính thì có thể chọn một vô nhì chế độ : DEG (hoặc D) viết tắt của Degree (độ) và RAD (hoặc R) viết tắt của Radian (Rad) (Nhìn kỹ bên trên màn hình máy tính có thể thấy chữ D hoặc R nhỏ xíu)

Nếu dùng chế độ D thì $\sin 30=0,5$ (vì Khi đó máy hiểu ngầm $30$ tức là $30^o$)

Còn nếu dùng chế độ R thì $\sin 30\approx -0,988031624$ (vì lúc đó máy hiểu ngầm $30$ là $30\ rad$)

Còn các công thức thì vẫn bình thường, chẳng hạn :

$\sin45^o=\cos45^o=\frac{\sqrt{2}}{2}$

$\cos\frac{\pi}{6}=\frac{\sqrt{3}}{2}$

$\sin1\approx 0,841470984$

$\sin1^o\approx 0,017452406$

Vậy nếu như x với đơn vị chức năng là chừng, thì máy tiếp tục tự động hóa gửi về radian.

Cảm ơn chúng ta nhiều nhé  .

Bài ghi chép và đã được sửa đổi nội dung vì chưng Tongkhangte: 05-08-2017 - 21:56

Ý bản thân là, nếu như x có mức giá trị như nhau tuy nhiên chỉ không giống đơn vị chức năng là chừng và radian, thì công thức bên trên với đổi khác gì làm cho đi ra nhì thành phẩm không giống nhau? 

Độ hoặc radian thì nó chỉ sai sự so sánh một hệ số nhân là $\frac{\pi}{180}$

($x^o$ thì tương ứng $x.\frac{\pi}{180}$ radian)

Nếu muốn tính bằng độ thì vô 2 công thức đó, vế trái giữ nguyên vẹn, còn vế phải chỗ nào có $x$ thì thay cho bằng $x.\frac{\pi}{180}$.

Nhưng làm như vậy thì công thức "cồng kềnh" quá. Tính bằng radian tiện rộng lớn nhiều (chỉ cần đổi độ thanh lịch rad, cũng đơn giản mà)

Mình sửa lại câu vấn đáp trước cơ rồi bạn  . Cảm ơn chúng ta vì như thế đã hỗ trợ.

Bài ghi chép và đã được sửa đổi nội dung vì chưng Tongkhangte: 05-08-2017 - 22:11